reading-notes

Linear Regressions

SOURCES

VIDEOS

Introduction to Simple Linear Regressions

ARTICLES

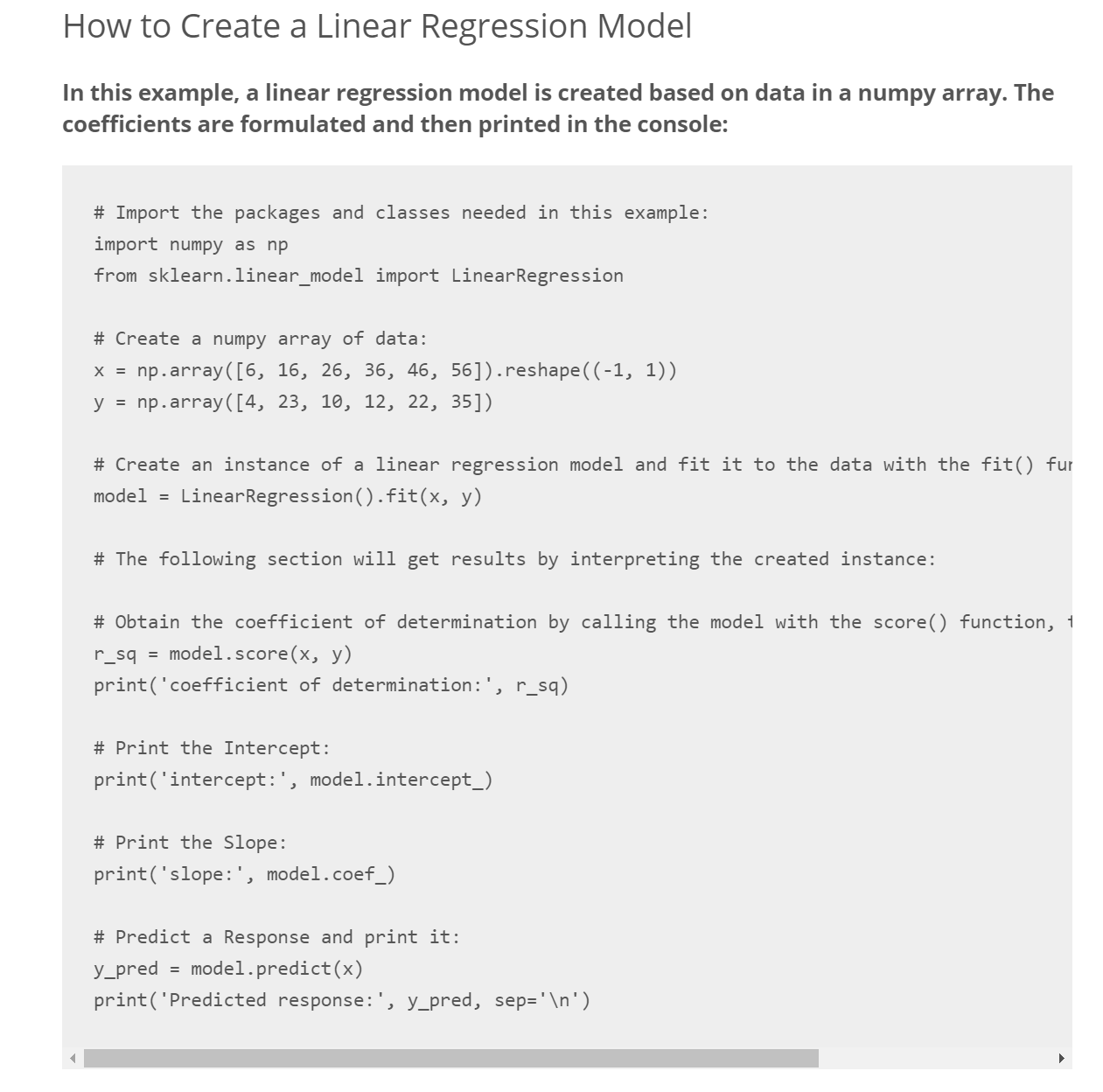
How to Run Linear Regression in Python

NOTES

• to understand linear regressions, we are gonna need to know some math
• *Key Concepts:
  • Best Fit – the straight line in a plot that minimizes the deviation between related scattered data points.
  • Coefficient – also known as a parameter, is the factor a variable is multiplied by. In linear regression, a coefficient represents changes in a Response Variable (see below).
  • Coefficient of Determination – the correlation coefficient denoted as 𝑅². Used to describe the precision or degree of fit in a regression.
  • Correlation – the relationship between two variables in terms of quantifiable strength and degree, often referred to as the ‘degree of correlation’. Values range between -1.0 and 1.0.
  • Dependent Feature – a variable denoted as y in the slope equation y=ax+b. Also known as an Output, or a Response.
  • Estimated Regression Line – the straight line that best fits a set of scattered data points.
  • Independent Feature – a variable denoted as x in the slope equation y=ax+b. Also known as an Input, or a predictor.
  • Intercept – the location where the Slope intercepts the Y-axis denoted b in the slope equation y=ax+b.
  • Least Squares – a method of estimating a Best Fit to data, by minimizing the sum of the squares of the differences between observed and estimated values.
  • Mean – an average of a set of numbers, but in linear regression, Mean is modeled by a linear function.
  • Ordinary Least Squares Regression (OLS) – more commonly known as Linear Regression.
  • Residual – vertical distance between a data point and the line of regression (see Residual in Figure 1 below).
  • Regression – estimate of predictive change in a variable in relation to changes in other variables (see Predicted Response in Figure 1 below).
  • Regression Model – the ideal formula for approximating a regression.
  • Response Variables – includes both the Predicted Response (the value predicted by the regression) and the Actual Response, which is the actual value of the data point (see Figure 1 below).
  • Slope – the steepness of a line of regression. Slope and Intercept can be used to define the linear relationship between two variables: y=ax+b.
  • Simple Linear Regression – a linear regression that has a single independent variable.